四年制世界杯已经开始

那么世界杯中有趣的数学问题是什么？

让我们一起看看

问题1：以下是世界杯年。这些数字的特征是什么？

1930，1934，1938，1954，1954，1958，1962，1966，1970，1974，1978，1978，1982，1986，1990，1994，1994，1998，2002，2006，2006，2006，2010，2014，2014，2014

你不明白吗？

这个学术大师知道！

答案：这些年是普通的年份，因为这些数字都不能分为4，因此这是普遍的年。然后四年后仍然是普遍的年份。

问题2：有32个国家参加了卡塔尔世界杯足球比赛（通常称为前32名），每个四个球队都在一个小组中。在第一轮单一循环赛中，每个国家都必须并且只能与小组中其他国家 /地区一起玩一场比赛。在前16名之后，它进入了淘汰赛。每两个国家都使用一场比赛来确定获胜者，前8名，前4名，最终获得冠军，亚军，第三和第四名将被决定。

在这一点上，这次世界杯的所有比赛都结束了。根据上述信息，计算后，有多少场世界杯足球比赛？

你不明白吗？

那个学术大师知道！

答：以卡塔尔世界杯为例，将32支球队分为8组。每组4个团队。每个小组将参加一次循环比赛，前2名将进步。

每个小组中的每个团队都必须与剩下的球队一起玩一场比赛，因此这是3场比赛。因此，每个组需要为3+2+1 = 6（场）或4×3÷2 = 6（field）。

在这里，可以使用树图，列表，连接等获得结果。这是卡塔尔 - 厄瓜多尔和厄瓜多尔 - 卡塔尔是同一游戏。

如果这是一场双圆形旋转比赛，那么这里有主场比赛。卡塔尔 - 厄瓜多尔和厄瓜多尔 - 卡塔尔应该有两场比赛。因此有4×3 = 12（字段）。

如果N球队参加一场循环比赛，则每个团队都必须参加（N-1）比赛，因此总共n（n-1）÷2场比赛；

如果N球队参加了双循环比赛，则必须总共进行N（N-1）比赛。

如果N球队参加淘汰赛，请参加比赛（N-1）比赛。

答案是正确的，请鼓掌！

流行科学知识：

一轮循环：参加比赛的所有球队都可以见面一次，每两个球队之间只能进行一场比赛。

一轮循环：参加比赛的所有球队都可以见面一次，每两个球队之间只能进行一场比赛。

双回合：双轮双回合所有球队都可以遇到两个，最后，根据两轮比赛的所有比赛的得分，得分和积分排名。

淘汰赛：如果输了，您将被淘汰，如果您获胜，您将继续比赛。

问题3：球队必须在世界杯上至少打3场比赛。由于小组赛是一场循环赛，因此需要与剩下的三支球队进行比赛。球队可以在世界杯上打几场比赛？

你不明白吗？

这个学术大师知道！

答：总共玩了7场比赛，其中包括三个小组赛，前16名，前8名和前4名冠军赛。 （如图所示）

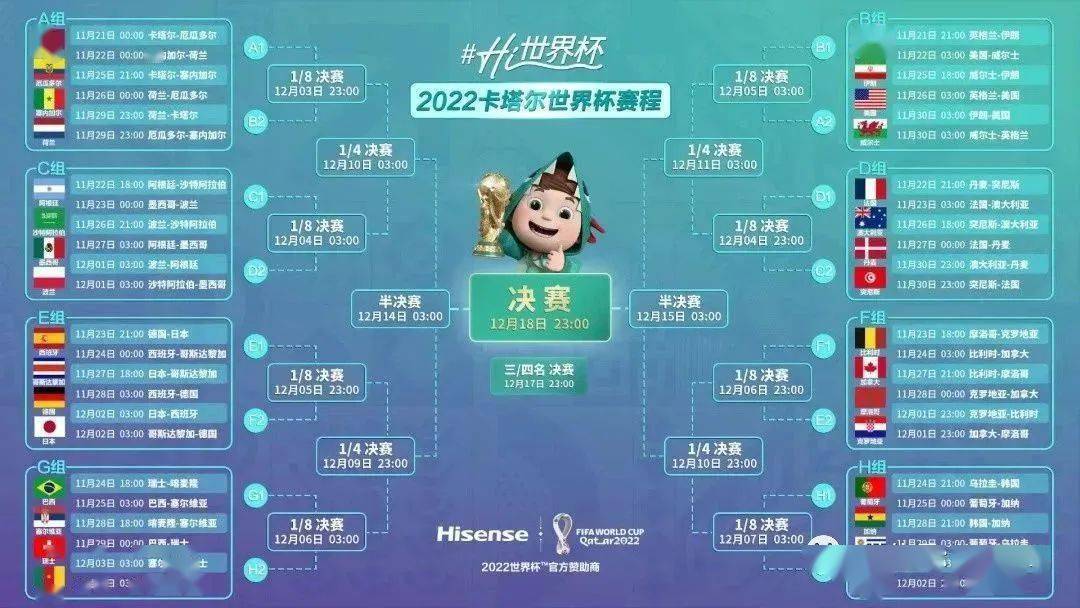
问题4：有多少球队在世界杯上打了7场比赛？

你不明白吗？

顶级学生知道！

答：由于决定了世界杯三到四个位置，因此前四支球队都将打7场比赛。

问题5：这些球队在世界杯上玩了多少场比赛？

你不明白吗？

那个学术大师知道！

答：16个球队被淘汰，只有3场比赛才返回家中；

8支球队将打4场比赛，进入前16名后，将淘汰一场比赛。

4支球队将打5场比赛，进入四分之一决赛后，将淘汰一场比赛。

进入前四名的四支球队将打7场比赛。半决赛中的一场比赛将首先进行；进入决赛的两支球队将打一场比赛以决定冠军。未进入决赛的两个球队也将争夺3或4个。

问题6：这些球队在世界杯上玩了多少场比赛？

你不明白吗？

那个学术大师知道！

答：自1998年世界杯以来，每节课总共举行了64场比赛。

世界杯分为小组阶段和淘汰赛阶段。

小组赛是一场循环赛，每个小组中有4个球队参加6场比赛。 8组共有8×6 = 48（游戏）；

每个小组的前2名进入淘汰赛阶段，共有16支球队。冠军是确定的，16-1 = 15场比赛，必须确定第三和第四名，还有另一场比赛，在淘汰赛中总共有15+1 = 16场比赛。

总共有48+16 = 64场比赛。

问题8：根据世界杯小组赛的规则，每个小组都有4支球队在单场比赛中，每个球队都有3场比赛，在小组中共有6场比赛。获胜的球队在每场比赛中得分3分，输的球队得分为0分，两支球队在平局中分别得到1分。在小组赛之后，两支球队最高得分都有资格。如果积分是相同的，那么具有更多进球的球队将会获胜。您知道该小组是否肯定有资格或基本上有资格？

你不明白吗？

这个学术大师知道！

答案：首先做出假设：假设每场比赛中获胜，绘画和输球的可能性是相同的，并且是1/3。

首先，您肯定会获得7分。因为每场比赛后两支球队的得分总数为2分（即，得分）或3分（有赢家）。因此，在小组中6场比赛后，每个团队的总分将不超过18分。如果一支球队获得7分，那么其余三支球队的总得分将不超过11​​分，而且两个球队的得分不可能大于或等于7分，因此该球队必须获得资格。

其次，您基本上可以获得6或5分。因为，如果一支球队获得6分，他们通常会有资格。只有当三支球队以同样的方式获得6分，而一支球队获得0分才能取消6分。假设A赢了B和C和C和C，则不可能产生0分，只有B和C才能获得0分。有两种情况，条件概率为2/27。这三支球队共同获得6分，A队的可能性排名第三，为1/3。因此，A团队A排名第三的有条件概率是2/81，也就是说，A团队A排名6分的概率为79/81。同样，排位赛的概率为5分为79/81。

最后，还有可能获得4或3分的资格。

但是，对于那些有2分，1分或0分的人来说，有资格是不可能的。

哔哔声---时间到了。

知识竞赛正式结束。

祝贺这位学术硕士，请上台获得该奖项！